Just because time is relative does not mean time is subjective. Time is a fundamental objective part of reality, and time and distance relativity is probably less weird than you think it is. There …
Hey, you seem to have a better understanding of the stuff, so perhaps you could point me in the right direction? Here’s my confusion: Let’s say at the inception of the earth, a clock started ticking (event 1), and let’s count earth’s age as up to the moment I made the post right next to that same clock (event 2). By special relativity (so obviously ignoring gravity etc), the interval between the two events is s^2 = t^2 - x^2 where t is the time elapsed on the clock, and x = 0 is the distance traveled by the clock in its own frame (earth’s frame), which is zero. For an observer moving at a constant speed relative to earth, the clock has moved, so x' != 0 (using ' for the moving frame), but the interval s is the same in both frames, so the time elapsed in the moving observer’s frame, between the same two events, must be greater than on the earth clock, t'^2 = s^2 + x'^2 > s^2 = t^2. In other words earth appears older (as measured by the relative time between the said two events) to the moving observer than to someone living on earth. This is where my comment about “two points in time” come from: without the spatial information, I wouldn’t be able to compare different relative times and pick its maximum.
I’m obviously not an astrophysicist and not familiar with the “well understood facts by astrophysicists” of maximum relative time/space. I suspect from your comment that my interpretation of “relative time” is wrong, but if you could point me to some accessible references, that would be very much appreciated!
I think your problem was you forgot the γ factor, which is still present even when using natural units. Or as the wiki describes it: “As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths.”
Edit: oh wait, you would still be upset that t’ = γT > T = t. Ok then! So using this diagram for example, two time units pass between O and P along the Earth’s red time axis, but 3 time units pass along the spaceship’s green prime time axis, and this is in conflict with the article’s claim that the Earth’s frame is the frame with the maximum rate of time.
I think the author meant to say you should calculate the time elapsed along the path that ends up back at the same point. If the spaceship were to turn around and return, 6 time units will have elapsed for it here, but 7 time units on earth. I.e. we are in the Twin’s Paradox/relativity of simultaneity territory here, but the important thing is that there is no path for the spaceship where you would see 7 or more time units elapsed, other than staying on Earth.
Thanks, I think we are actually in agreement here: if you account for the fact that \gamma>1 in general, then your calculation showed that T' = \gamma T > T, that is, the moving observer in general registers a longer duration T' between the two events than the clock at rest (T). I was just taking a shortcut when I said this should follow from X' != 0 (the -\gamma v T in your calculation).
Also, thanks for the imagery of aliens taking earth for a joy ride. This might be how we are saved when the sun dies.
Edit: I think we agree on both accounts as the twin paradox is also the only way I can rationalize the original claim (even said so in my first reply)
twin paradox is also the only way I can rationalize the original claim
The fact that there is a maximum amount of relative time that can elapse between any 2 “events” does not rely on the twin paradox in any way. It doesn’t even depend on movement at all since there is gravitational time dilation and the 2 events don’t even need to be “witnessed” for time to have a particular relative duration between the events. Whichever of 2 different inertial frames of reference has the least amount of gravitational time dilation has the faster time flow rate and is closest to the maximum rate.
If a piece of matter had no gravitational time dilation at all (which admittedly is impossible) what would be the time flow rate for the object? For simplicity let’s assume it is not accelerating or even moving at all (except for expansion of universe). How would we know it is not moving? Let’s assume (call it a thought experiment) that the universe has a center and boundaries, and that the distance and direction to the center is not changing. This object would have no time dilation, the maximum time flow rate, and experience the longest possible duration of time across any arbitrary points in time.
In other words earth appears older (as measured by the relative time between the said two events) to the moving observer than to someone living on earth.
It’s fine and to be expected that time passes differently with different levels of time dilation. You might have Reference Frame A where the time flow rate is 99.999% of the maximum and Frame B where the time flow rate is 99.998% of the maximum. The time flow rate in Frame A is faster than B, because A is closer to the maximum rate than B.
This is where my comment about “two points in time” come from:
Think of “two points in time” as 2 events in time, and (for simplicity) at the same fixed point in space in your frame of reference (A) and another person’s frame of reference (B). Whichever frame is under the greater influence of gravitational time dilation, will have a slower time flow rate than the other frame. But there is also a maximum amount of time between the 2 events that neither of those 2 frames (or any other frame of reference) can exceed.
without the spatial information, I wouldn’t be able to compare different relative times and pick its maximum.
Figuring out the maximum time flow rate between any 2 events or points in time would not be a simple thing at all. You would have to calculate the entire amount of gravitational time dilation of every gravity field in range of your object, and add to that the total amount of time dilation due to acceleration of your object. But just because the total amount of time dilation is not a simple thing to calculate and add to your equations, does not mean that “zero time dilation” == “maximum time flow rate” does not exist nor that there is not a maximum amount of relative time duration between any 2 events/point in time. I assume you agree that there is a maximum amount of relative distance between any 2 objects/points in space right? There is also a maximum amount of relative duration between any 2 events/points in time. And the length contraction that shrinks distance length is related to the time dilation that shrinks time duration.
but if you could point me to some accessible references that would be very much appreciated!
I hate to mention reddit here but this reddit comment explains it better than I can.
[It’s likely based on the proper time of a comoving observer in simplified cosmological solutions of general relativity. A comoving observer is an observer whose ‘motion’ is due to the expansion of the universe, not any motion with respect to the comoving frame. The cosmological solutions are also isotropic and homogenous, so there are no clumps of matter like black holes to influence time - the comoving proper time is the same everywhere and can be considered a maximum time.]
Hey, you seem to have a better understanding of the stuff, so perhaps you could point me in the right direction? Here’s my confusion: Let’s say at the inception of the earth, a clock started ticking (event 1), and let’s count earth’s age as up to the moment I made the post right next to that same clock (event 2). By special relativity (so obviously ignoring gravity etc), the interval between the two events is
s^2 = t^2 - x^2wheretis the time elapsed on the clock, andx = 0is the distance traveled by the clock in its own frame (earth’s frame), which is zero. For an observer moving at a constant speed relative to earth, the clock has moved, sox' != 0(using'for the moving frame), but the intervalsis the same in both frames, so the time elapsed in the moving observer’s frame, between the same two events, must be greater than on the earth clock,t'^2 = s^2 + x'^2 > s^2 = t^2. In other words earth appears older (as measured by the relative time between the said two events) to the moving observer than to someone living on earth. This is where my comment about “two points in time” come from: without the spatial information, I wouldn’t be able to compare different relative times and pick its maximum.I’m obviously not an astrophysicist and not familiar with the “well understood facts by astrophysicists” of maximum relative time/space. I suspect from your comment that my interpretation of “relative time” is wrong, but if you could point me to some accessible references, that would be very much appreciated!
Using the Lorenz transformation formula, here’s what I get:
γ = 1/sqrt(1 - (v/c)^2) Δs^2 = (cΔt)^2 - Δx^2 ct' = γ (ct - (v/c)x) x' = γ (x - vt)In the Earth’s reference frame, the planet starts at (t=0,x=0) and just stays still for time T (say 4.5 billion years):
In the spaceship’s prime frame, we get:
p_i' = (0,0) p_f' = (γT, -γvT) s'^2 = (cγT)^2 - (-γvT)^2 = γ^2 T^2 (c^2 - v^2) = T^2 (c^2 - v^2) / (1 - v^2/c^2) = T^2 (c^2 - v^2) / (c^2 - v^2) * c^2 = (cT)^2I think your problem was you forgot the γ factor, which is still present even when using natural units. Or as the wiki describes it: “As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths.”
Edit: oh wait, you would still be upset that t’ = γT > T = t. Ok then! So using this diagram for example, two time units pass between O and P along the Earth’s red time axis, but 3 time units pass along the spaceship’s green prime time axis, and this is in conflict with the article’s claim that the Earth’s frame is the frame with the maximum rate of time.
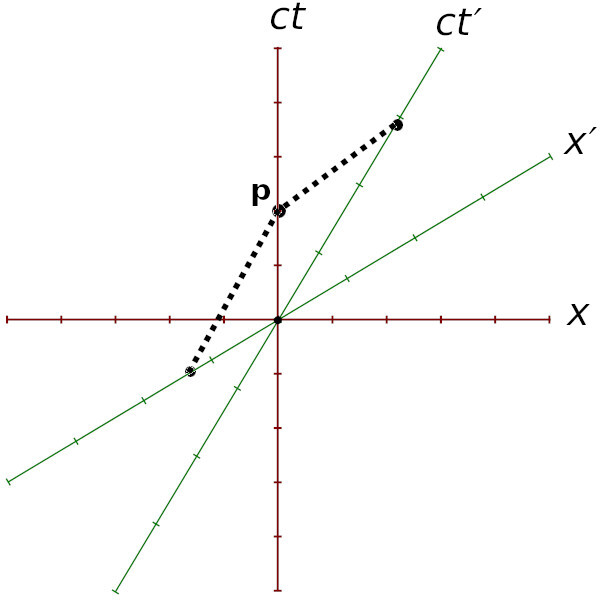
I think the author meant to say you should calculate the time elapsed along the path that ends up back at the same point. If the spaceship were to turn around and return, 6 time units will have elapsed for it here, but 7 time units on earth. I.e. we are in the Twin’s Paradox/relativity of simultaneity territory here, but the important thing is that there is no path for the spaceship where you would see 7 or more time units elapsed, other than staying on Earth.
Thanks, I think we are actually in agreement here: if you account for the fact that
\gamma > 1in general, then your calculation showed thatT' = \gamma T > T, that is, the moving observer in general registers a longer durationT'between the two events than the clock at rest (T). I was just taking a shortcut when I said this should follow fromX' != 0(the-\gamma v Tin your calculation).Also, thanks for the imagery of aliens taking earth for a joy ride. This might be how we are saved when the sun dies.
Edit: I think we agree on both accounts as the twin paradox is also the only way I can rationalize the original claim (even said so in my first reply)
The fact that there is a maximum amount of relative time that can elapse between any 2 “events” does not rely on the twin paradox in any way. It doesn’t even depend on movement at all since there is gravitational time dilation and the 2 events don’t even need to be “witnessed” for time to have a particular relative duration between the events. Whichever of 2 different inertial frames of reference has the least amount of gravitational time dilation has the faster time flow rate and is closest to the maximum rate.
If a piece of matter had no gravitational time dilation at all (which admittedly is impossible) what would be the time flow rate for the object? For simplicity let’s assume it is not accelerating or even moving at all (except for expansion of universe). How would we know it is not moving? Let’s assume (call it a thought experiment) that the universe has a center and boundaries, and that the distance and direction to the center is not changing. This object would have no time dilation, the maximum time flow rate, and experience the longest possible duration of time across any arbitrary points in time.
That was exactly the point, although I think there are also other ways to prove it. Thanks for expressing this better than I.
It’s fine and to be expected that time passes differently with different levels of time dilation. You might have Reference Frame A where the time flow rate is 99.999% of the maximum and Frame B where the time flow rate is 99.998% of the maximum. The time flow rate in Frame A is faster than B, because A is closer to the maximum rate than B.
Think of “two points in time” as 2 events in time, and (for simplicity) at the same fixed point in space in your frame of reference (A) and another person’s frame of reference (B). Whichever frame is under the greater influence of gravitational time dilation, will have a slower time flow rate than the other frame. But there is also a maximum amount of time between the 2 events that neither of those 2 frames (or any other frame of reference) can exceed.
Figuring out the maximum time flow rate between any 2 events or points in time would not be a simple thing at all. You would have to calculate the entire amount of gravitational time dilation of every gravity field in range of your object, and add to that the total amount of time dilation due to acceleration of your object. But just because the total amount of time dilation is not a simple thing to calculate and add to your equations, does not mean that “zero time dilation” == “maximum time flow rate” does not exist nor that there is not a maximum amount of relative time duration between any 2 events/point in time. I assume you agree that there is a maximum amount of relative distance between any 2 objects/points in space right? There is also a maximum amount of relative duration between any 2 events/points in time. And the length contraction that shrinks distance length is related to the time dilation that shrinks time duration.
I hate to mention reddit here but this reddit comment explains it better than I can.
https://www.reddit.com/r/cosmology/comments/14dg7yf/saying_that_the_universe_is_138_billion_years_old/joq3n5i/
[It’s likely based on the proper time of a comoving observer in simplified cosmological solutions of general relativity. A comoving observer is an observer whose ‘motion’ is due to the expansion of the universe, not any motion with respect to the comoving frame. The cosmological solutions are also isotropic and homogenous, so there are no clumps of matter like black holes to influence time - the comoving proper time is the same everywhere and can be considered a maximum time.]