Today there’s an abundance of textbooks and webbooks on Bayesian probability theory, decision theory, and statistics, at very diverse technical levels. I wanted to point out three books whose main topic is not probability theory, but which give very good introductions (even superior to those of some specialized textbooks, in my opinion) to Bayesian probability theory:
-
Artificial Intelligence: A Modern Approach by S. J. Russell, P. Norvig. Part IV is an amazing introduction to Bayesian theory – including decision theory – with many connections with Artificial Intelligence and Logic.
-
Medical Decision Making by H. C. Sox, M. C. Higgins, D. K. Owens. This is essentially a very clear and insightful textbook on Bayesian probability theory and decision theory, but targeted to clinical decision-making.
-
Sentential Probability Logic: Origins, Development, Current Status, and Technical Applications by T. Hailperin. This is a book on Bayesian probability theory, presented as a generalization of propositional logic. This point of view is the most powerful I know of. The books also has important results on methods to find probability bounds, and on combining evidence.

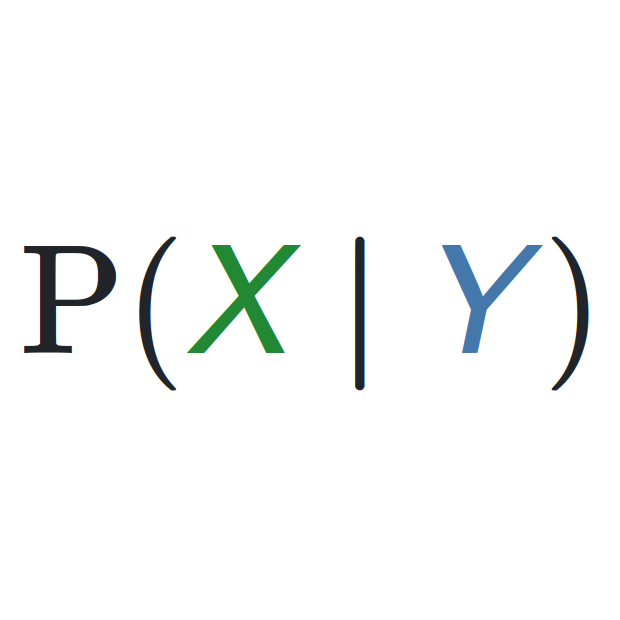
I believe that “superficial knowledge” is the best starting point :) It gives you more opportunities to understand things with a fresh look, and see things that people with “less superficial” knowledge don’t see anymore. Because unfortunately there’s always a process of routine-building and fossilization going on in parallel with knowledge acquisition.
The fluorescence problem sounds cool! The point is that every classification involves some uncertainty, which in some cases can’t be reduced under a certain amount, no matter how many training data one uses. Extreme example: even if we give quadrillions of training data about an ordinary tossed coin to some algorithm, the algorithm will never be able to get more than 50% right at the next toss. So, training is good, but it only addresses part of the problem, and only up to a certain point.
What becomes important next, is how good or bad it is to make the wrong decision/classification, owing to the uncertainty. In some situations it’s best to avoid predicting something that’s not the case (say, a pixel that’s not a target cell); in others it’s best to be on the safe side (better to have some false pixels than to lose even just one target cell). What’s best is very problem-dependent, even when the data are the same. It depends on what further use the classification will have. This aspect is, at present, something that training processes don’t take into account very much.
Artificial Intelligence gives a very insightful perspective and a systematic framework for the whole problem :)
Well, sorry for the babble – good luck with the research!
This makes me think about stock traders who are trying to build AI models to optimize their trading strategy. I can’t say that they are wrong, and sure, why not, I encourage them to try… But I think they are dealing with a very similar problem to a coin toss.
Oh, don’t apologize for that!! And thank you :D